Baire Spaces

This expository blog post on Baire Spaces was my submission as a project for a topology course taught by Professor Mike Miller Eismeier at Columbia University. A prospective reader should have done a first course in topology and analysis; everything else is developed from scratch. I have freely borrowed and modified from all the references listed at the end.

“The Baire category is a profound triviality which condenses the folk wisdom of a generation of ingenious mathematicians into a single statement.” Tom Körner (Körner, 2008)

INTRODUCTION

Every mathematician has a few tricks (Rota, 2008) which form the foundation of their toolkit that they apply skilfully to a great variety of problems (Tao, 2021). One of the goals of this expository blog post is to convince the reader that Baire category theorems are a worthwhile addition to their toolkit. The other goal is to simply indulge in the study of Baire spaces for it is beautiful mathematics.

Small Sets

What is a “small” set? This question can have multiple answers depending on whom you ask. For a set theorist, a countable set is small, while for an analyst, a set of measure $0$ is small. We will see that for a topologist the ideas of nowhere dense set and meager set encapsulate the notion of smallness. These different notions of smallness don't always coincide though. For example, Cantor set is an uncountable set having Lebesgue measure $0$ , and as we will see in Section 2 it is also nowhere dense in $\mathbb R.$

Using this topological vocabulary for small sets we will define the notion of a Baire space, which in this vocabulary aren't small. Many well-behaved classes of spaces are Baire. Among the most well-known are locally compact Hausdorff spaces and complete pseudometric spaces. This is the content of the famous Baire category theorems which will be the highlight of this blog post.

These Baire category theorems are a powerful class of results useful for proving existence. We will see in Section 7 how they can be applied to prove existence of objects of desired property. The main idea which these applications follow is to first construct a set $X$ in which we want to prove there exist elements satisfying a certain property, and then show that elements not satisfying this property, in fact, form a small set.

Warm-Up

As a warm-up to the kind of arguments we will be dealing with let's show that every nonempty compact Hausdorff space with no isolated points is uncountable. This will in particular show that $[0,1]$ is uncountable.

We first show that given any nonempty open set $U$ of $X$ and any point $x \in X$ , there exists a nonempty open set $V$ contained in $U$ such that $x$ is not contained in the closure $\mathrm{cl}_X(V)$ of $V$ in $X.$ If $x \in U$ , then since $\{x\}$ is not open, $U$ must contain a point different from $x.$ On other hand, if $x \notin U$ , then since $U$ is nonempty it must contain a point different from $x.$ In either case denote this point by $y.$ $X$ is Hausdorff, and therefore we can choose two disjoint open subsets $W_1, W_2$ of $X$ such that $x \in W_1$ and $y \in W_2.$ Then let $V = W_2 \cap U.$ It is an open set contained in $U$ , it is nonempty because it contains $y$ , and its closure does not contain $x.$

To finish proving that $X$ is uncountable we show that any given function $f \colon \mathbb N \to X$ is not surjective. Let $x_n = f(n).$ Apply our result above to the nonempty open set $U = X$ to choose a nonempty open subset $V_1$ of $X$ such that $x_1 \notin \mathrm{cl}_X(V_1).$ In general, for each $n \in \mathbb N,$ given nonempty open subset $V_{n}$ of $X$ , choose $V_{n+1}$ using the result above such that $V_{n+1} \subseteq V_n$ and $x_{n+1} \notin \mathrm{cl}_X(V_{n+1}).$ We get a nested sequence

\mathrm{cl}_X(V_1) \supseteq \mathrm{cl}_X(V_2) \supseteq \cdots

of nonempty closed subsets of $X.$ Now recall the classical result that a topological space $X$ is compact if and only if for every collection $\mathcal{C}$ of closed subsets of $X$ having the finite intersection property (i.e., every finite sub-collection of $\mathcal{C}$ has nonempty intersection), the intersection $\bigcap_{C \in \mathcal{C}} C$ is nonempty (See Proposition 5.4 for a proof). Therefore, there exists a point $x \in \bigcap_n \mathrm{cl}_X(V_n).$ Now $x$ cannot equal $x_n$ for any $n \in \mathbb N,$ since $x$ is in $\mathrm{cl}_X(V_n)$ but $x_n$ is not. Therefore, $f$ is not surjective.

We showed that $X$ cannot be written as a countable union of singletons. A compact Hausdorff space is $T_1$ , i.e., for any $x \in X$ , the singleton $\{x\}$ is closed. We will show later that the singletons $\{x\}$ in this case are what is called nowhere dense, and that $X$ cannot be written as a countable union of nowhere dense sets. This is exactly the content of Baire category theorems, and therefore we could have concluded uncountability directly from these theorems.

PREREQUISITES

In this section we give a brief tour of the prerequisites from point-set topology, mainly for notational convenience. For a more comprehensive treatment see the excellent textbooks (Munkres, 2000), (Willard, 2004), (Engelking, 1989).

We start by recalling the notions of interior and closure which will be used in defining the notions of dense and nowhere dense sets in a topological space. As we mentioned before they provide a topological vocabulary to deal with “large” and “small” sets. Throughout we simply write $X$ for a topological space $(X, \mathcal{T}).$

Definition 2.1 (Interior and Closure): Given a subset

S

of a topological space

X

, the interior of $S$ in $X$ , denoted

\mathrm{int}_X(S)

, is defined as the union of all open sets contained in

S

, and the closure of $S$ in $X$ , denoted

\mathrm{cl}_X(S)

, is defined as the intersection of all closed sets containing

S.

Note that $\mathrm{int}_X(S)$ is an open set in $X$ and $\mathrm{cl}_X(S)$ is a closed set in $X.$ The reason for our cumbersome but informative notation, as opposed to the commonly used concise but uninformative notation $S^\circ$ and $\overline{S}$ for interior and closure respectively, will become clear later as we take interiors and closures under different topological spaces. It also emphasizes the important point that these operations depend on the topological space; for example, $\mathrm{int}_{\mathbb R}(\mathbb R) = \mathbb R$ but $\mathrm{int}_{\mathbb R^2}(\mathbb R) = \varnothing.$

Proposition 2.2 (Equivalent characterization of closure): Given a subset

S

of a topological space

X

x \in \mathrm{cl}_X(S)

if and only if every open subset

U

X

containing

x

intersects

S.

We show that

x \notin \mathrm{cl}_X(S)

if and only if there exists an open subset

U

X

containing

x

that does not intersect

S.

x \notin \mathrm{cl}_X(S),

the set

U = X \setminus \mathrm{cl}_X(S)

is an open subset of

X

containing

x

that does not intersect

S.

Conversely, if there exists an open subset

U

X

containing

x

that does not intersect

S,

then

X \setminus U

is a closed subset of

X

containing

S.

By the definition of the closure, the set

X \setminus U

must contain

\mathrm{cl}_X(S)

, implying

x \notin \mathrm{cl}_X(S).

Proposition 2.3 (Complements of interior and closure): For any subset

S

of a topological space

X,

X \setminus \mathrm{int}_X(S) = \mathrm{cl}_X(X \setminus S)

and

X \setminus \mathrm{cl}_X(S) = \mathrm{int}_X(X \setminus S).

This follows immediately from the definitions of closure and interior, and the De Morgan's laws:

\begin{aligned} X \setminus \mathrm{int}_X(S) &= X \setminus \bigcup_{\substack{U \subseteq S \\ U \text{ open in } X}} U = \bigcap_{\substack{U \subseteq S \\ U \text{ open in } X}} (X \setminus U) = \bigcap_{\substack{X \setminus U \supseteq X \setminus S \\ X \setminus U \text{ closed in } X}} (X \setminus U) = \bigcap_{\substack{C \supseteq X \setminus S \\ C \text{ closed in } X}} C = \mathrm{cl}_X(X \setminus S), \\ X \setminus \mathrm{cl}_X(S) &= X \setminus \bigcap_{\substack{C \supseteq S \\ C \text{ closed in } X}} C = \bigcup_{\substack{C \supseteq S \\ C \text{ closed in } X}} (X \setminus C) = \bigcup_{\substack{X \setminus C \subseteq X \setminus S \\ X \setminus C \text{ open in } X}} (X \setminus C) = \bigcup_{\substack{U \subseteq X \setminus S \\ U \text{ open in } X}} U = \mathrm{int}_X(X \setminus S). \end{aligned}

Definition 2.4 (Dense and nowhere dense): A subset

S

of a topological space

X

is said to be dense in $X$ if its closure equals

X

, i.e.,

\mathrm{cl}_X(S)=X.

S

is called nowhere dense or rare in $X$ if its closure has empty interior, i.e.,

\mathrm{int}_X(\mathrm{cl}_X(S)) = \varnothing.

Nowhere dense sets give a precise meaning to “sparsely populated sets” or “sets with holes” (see the characterization in Proposition 2.7 (c) for a more concrete depiction of this). Nowhere dense is a strengthening of the condition “not dense” (every nowhere dense set is not dense, but the converse is false).

We immediately give equivalent characterizations of dense and nowhere dense sets which we will freely use.

Proposition 2.5 (Equivalent characterizations of dense sets): Let

S

be a subset of the topological space

X.

Then

S

is dense in

X

if and only if

S

has nonempty intersection with every nonempty open subset of

X.

S

is dense in

X

means

\mathrm{cl}_X(S) = X,

which using Proposition 2.3 can written as

\mathrm{int}_X(X \setminus S) = \varnothing.

By the definition of interior this means that the only open set disjoint from

S

is the empty set.

In the next proposition, and anywhere else, unless specified otherwise, a subspace is endowed with the subspace topology.

Proposition 2.6 (Dense subset of a dense set is itself dense): Suppose

X

is a topological space and

T \subseteq S \subseteq X

are subspaces with

T

dense in

S

and

S

dense in

X.

Then

T

is dense in

X.

Let

U

be a nonempty open subset of

X.

Then

U \cap S

in nonempty by Proposition 5. Now note that

U \cap S

is an open subset of

S

in the subspace topology, and therefore

(U \cap S) \cap T

is also nonempty. But this implies that

T

is dense in

X.

Proposition 2.7 (Equivalent characterisations of nowhere dense sets): Let $S$ be a subset of the topological space $X.$ Then the following are equivalent:

(a) $S$ is nowhere dense in $X.$

(b) $X \setminus \mathrm{cl}_X(S)$ is dense in $X.$

(d) $S$ is not dense in any nonempty open subset $U$ of $X.$

The proof is pretty simple and involves simple manipulation of the definitions.

$(a) \iff (b)$ : $S$ is nowhere dense in $X$ means $\mathrm{int}_X(\mathrm{cl}_X(S) = \varnothing,$ which using Proposition 3 can written as $\mathrm{cl}_X(X \setminus \mathrm{cl}_X(S)) = X,$ i.e., $X \setminus \mathrm{cl}_X(S)$ is dense in $X.$

$(b) \implies (c)$ : If $S = \varnothing$ then $(c)$ holds trivially, so suppose $S$ is nonempty. Then Propositions 3 and 5 imply that every nonempty open subset $U$ of $X$ intersects $\mathrm{int}_X(X \setminus S).$ Note that $\mathrm{int}_X(X \setminus S)$ is an open set disjoint from $S$ and thus we can let $V = U \cap \mathrm{int}_X(X \setminus S).$

$(c) \implies (b)$ : If every nonempty open subset $U$ of $X$ contains a nonempty open subset $V$ that is disjoint from $S,$ then every nonempty open subset $U$ of $X$ intersects the open set $\mathrm{int}_X(X \setminus S),$ which by Propositions 3 and 5 implies $(b).$

Example 2.8: These examples should help develop intuition.

The set of rationals $\mathbb Q$ is dense in $\mathbb R,$ and hence not nowhere dense in $\mathbb R.$
$\mathbb R$ is nowhere dense in $\mathbb R^n$ for $n > 1.$
The integers $\Z$ are nowhere dense in $\mathbb R.$ However, $\Z \cup (a,b)$ for $a < b \in \mathbb R$ is not nowhere dense in $\mathbb R$ since it is dense in $(a,b).$ $\Z \cup (a,b)$ is not dense in $\mathbb R$ either.
The set $S = \left\{\frac{1}{n}\right\}_{n \in \mathbb N}$ is nowhere dense in $\mathbb R,$ since its closure $\mathrm{cl}_{\mathbb R}(S) = S \cup \{0\}$ has empty interior in $\mathbb R.$
Suppose $X$ is a $T_1$ space, i.e., for any $x \in X,$ the singleton $\{x\}$ is closed, and suppose that the singletons are not isolated, i.e., for any $x \in X,$ the singleton $\{x\}$ is not open. Then singletons are nowhere dense. This is true, for example, if $X$ is $\mathbb R^n$ for any ${n \in \mathbb N}.$
The Cantor set $C$ is nowhere dense in $\mathbb R.$ To see this first recall that the Cantor set is constructed using the decreasing sequence $\{C_n\}_{n \ge 0}$ of closed sets defined as follows: $C_0 = [0,1],$ $C_1 = [0, 1/3] \cup [2/3, 1],$ $C_2 = [0, 1/9] \cup [2/9, 3/9] \cup [6/9, 7/9] \cup [8/9, 1],$ and so on, where at each step to get $C_{n+1}$ from $C_n$ we remove the middle third open interval from each of the $2^n$ closed disjoint subsets of $C_n.$ The Cantor set is the countable intersection $C = \bigcap_{n \in \mathbb N} C_n.$ $C$ is therefore nowhere dense since $C_n$ contains no interval of length greater than $1/3^n.$
Suppose $X$ is a topological space and $S \subseteq X.$ The boundary of $S$ in $X,$ denoted $\mathrm{bd}_X(S)$ is defined to be the closed set $\mathrm{cl}_X(S) \cap \mathrm{cl}_X(X \setminus S).$ The neighborhood of any point in $\mathrm{bd}_X(S)$ intersects both $S$ and $X \setminus S.$ Therefore, if $S$ is open in $X,$ $\mathrm{bd}_X(S) \subseteq X \setminus S,$ and thus $\mathrm{int}_X(\mathrm{bd}_X(S)) = \varnothing.$ Similarly, if $S$ is closed, $\mathrm{bd}_X(S) \subseteq S$ and thus $\mathrm{int}_X(\mathrm{bd}_X(S)) = \varnothing.$ In other words, boundaries of open or closed sets is nowhere dense, and also a closed set is nowhere dense if and only if it coincides with its boundary.

Properties Of Nowhere Dense Sets

We next define an ideal and a $\sigma-$ ideal. This definition will help us view many notions of “smallness” like being nowhere dense, being meager (see Definition 3.1), being countable, or having measure $0,$ as related.

Definition 2.9 (Ideal and $\sigma-$ ideal): An ideal on a set

X

is a collection of subsets of

X

containing

\varnothing

and closed under arbitrary subsets and finite unions. If the collection is also closed under countable unions it is called a $\sigma-$ ideal.

Proposition 2.10 (Nowhere dense sets form an ideal): The collection of nowhere dense sets in a topological space

X

is an ideal on

X.

The fact that a subset of a nowhere dense set in

X

is also nowhere dense in

X

is obvious. To prove that a finite union of nowhere dense sets in

X

is also nowhere dense in

X

we need only show that for two nowhere dense sets

S_1

and

S_2

X.

Using the characterization in Proposition 2.7 (c), for each nonempty open subset

U

X

we can find non-empty open subsets

U_1

and

U_2

X

such that

U_1 \subseteq U \setminus S_1

and

U_2 \subseteq U_1 \setminus S_2.

Hence

U_2 \subseteq U \setminus (S_1 \cup S_2),

and therefore again by Proposition 2.7 (c),

S_1 \cup S_2

is nowhere dense in

X.

The union of countably many nowhere dense sets may not be nowhere dense as the example of $\mathbb Q$ in $\mathbb R$ shows.

The next proposition will be useful since we will often have open or dense subsets.

Proposition 2.11 (Nowhere density for subspaces): Let

Y

be a subspace of a topological space

X,

and let

S

be a subset of

Y.

S

is nowhere dense in

Y,

then

S

is nowhere dense in

X.

Conversely, if

Y

is open or dense in

X

and

S

is nowhere dense in

X,

then

S

is nowhere dense in

Y.

Suppose first that $S$ is nowhere dense in $Y.$ Let $U$ be a nonempty open subset of $X$ that intersects $Y.$ Then $U \cap Y$ is open in $Y$ by the definition of subspace topology. By Proposition 2.7 there exists a nonempty open subset $V$ of $Y$ which is contained in $U \cap Y$ and is disjoint from $S.$ By the definition of subspace topology on $Y,$ there exists a nonempty open subset $W$ of $X$ such that $V = W \cap Y.$ This set is such that $W \cap S = \varnothing$ and can taken to be such that $W \subseteq U$ by taking its intersection with $U$ if necessary. By using Proposition 2.7 again we see that $S$ is nowhere dense in $X.$

Now suppose that $Y$ is open in $X$ and that $S$ is nowhere dense in $X.$ Let $U$ be any open subset of $Y,$ which, because $Y$ is open in $X,$ is then also open in $X.$ Therefore, by Proposition 2.7 there exists a nonempty open subset $V$ of $X$ which is contained in $U$ and is disjoint from $S.$ This set $V$ is open in $Y$ also because $V = V \cap Y.$ Therefore, by Proposition 2.7 again, $S$ is nowhere dense in $Y.$

Finally suppose that $Y$ is dense in $X$ and that $S$ is nowhere dense in $X.$ Let $U$ be any open subset of $Y.$ Then there exists an open subset $W$ of $X$ such that $U = W \cap Y.$ By Proposition 2.7 there exists a nonempty open subset $V$ of $X$ which is contained in $W$ and is disjoint from $S.$ We see that the set $V \cap Y$ is nonempty by noting that $Y$ is dense in $X$ and then using Proposition 2.5. It is also open in $Y,$ is contained in $U,$ and is disjoint from $S.$ By Proposition 2.7 then, $S$ is nowhere dense in $Y.$

How does nowhere density behave with respect to taking products? As the next theorem shows, the behaviour is simple under finite products. For infinite products an extra (intuitive) condition can cause the product to be nowhere dense. As an example of this condition, let $X_n = [0,1]$ and $S_n = [0,1/2]$ for each ${n \in \mathbb N}.$ Then for no ${n \in \mathbb N},$ is $S_n$ is nowhere dense in $X_n,$ but $\prod_{n \in \mathbb N} S_n$ is nowhere dense in $\prod_{n \in \mathbb N} X_n.$

Proposition 2.12 (Products of nowhere dense sets): Let $A$ be an index set. For all $\alpha \in A,$ let $X_\alpha$ be a topological space and let $S_\alpha \subseteq X_\alpha.$

If $A$ is finite, then $\prod_{\alpha \in A} S_\alpha$ is nowhere dense in $\prod_{\alpha \in A} X_\alpha$ if and only if there exists a $\beta \in A$ such that $S_\beta$ is nowhere dense in $X_\beta.$

If $A$ is infinite, then $\prod_{\alpha \in A} S_\alpha$ is nowhere dense in $\prod_{\alpha \in A} X_\alpha$ if and only if there exists a $\beta \in A$ such that $S_\beta$ is nowhere dense in $X_\beta$ or there exists infinitely many $\beta \in A$ such that for each such $\beta,$ $S_\beta$ is not dense in $X_\beta.$

First note that although the theorem is stated separately for $A$ finite and $A$ infinite, having only the second statement without the “If $A$ is infinite” is sufficient because the “or” part is redundant if $A$ is finite. For notational simplicity, let $X = \prod_{\alpha \in A} X_\alpha$ and $S = \prod_{\alpha \in A} S_\alpha.$

We start with proving the contrapositive of the if side. Suppose that for each $\alpha \in A,$ $\mathrm{int}_{X_\alpha}(\mathrm{cl}_{X_\alpha}(S_\alpha)) \neq \varnothing$ and that $\mathrm{cl}_{X_\alpha}(S_\alpha) = X_\alpha$ for all but finitely many $\alpha \in A.$ Then, using the definition of product topology, it is easily seen that

\mathrm{int}_{X}(\mathrm{cl}_{X}(S)) = \prod_{\alpha \in A} \mathrm{int}_{X_\alpha}(\mathrm{cl}_{X_\alpha}(S_\alpha)) \neq \varnothing,

thereby showing that $\prod_{\alpha \in A} S_\alpha$ is not nowhere dense in $\prod_{\alpha \in A} X_\alpha.$

For the other side, we split the analysis into two parts depending on which condition is true. If for some $\beta \in A,$ $S_\beta$ is nowhere dense in $X_\beta$ , i.e., $\mathrm{int}_{X_\beta}(\mathrm{cl}_{X_\beta}(S_\beta)) = \varnothing,$ then $\prod_{\alpha \in A} S_\alpha$ is nowhere dense in $\prod_{\alpha \in A} X_\alpha$ since

\mathrm{int}_X(\mathrm{cl}_X(S)) = \prod_{\alpha \in A} \mathrm{int}_{X_\alpha}(\mathrm{cl}_{X_\alpha}(S_\alpha)) = \varnothing.

On the other hand, if $\mathrm{cl}_{X_\beta}(S_\beta) \neq X_\beta$ for infinitely many $\beta \in A,$ and $U$ is any element from the canonical basis of the product topology on $X,$ then there exists a $\gamma \in A$ such that

\pi_\gamma(U) = X_\gamma \text{ and } \mathrm{cl}_{X_\gamma}(S_\gamma) \neq X_\gamma,

where $\pi_\gamma \colon X \to X_\gamma$ denotes the canonical projection. Define the nonempty open subset $V \subseteq U$ by

\pi_\gamma(V) = X_\gamma \setminus \mathrm{cl}_{X_\gamma}(S_\gamma) \text{ and } \pi_\alpha(V) = \pi_\alpha(U).

Then $V \cap S = \varnothing,$ showing that $S$ is nowhere dense in $X.$

MEAGER SETS

Definition 3.1 (Meager and nonmeager sets): A subset

S

of a topological space

X

is called meager or of first category in $X$ if it can be written as a countable union of nowhere dense sets in

X.

Otherwise,

S

is called nonmeager or of second category in $X.$

We will eschew the usage of the terminology “first category” or “second category” because aside from being non-descriptive, the word “category” in mathematics has “been conscripted for higher service” as S. Berberain remarked (Berberian, 1974).

Remark 3.2: By Proposition 2.11, if $Y$ is an open or a dense subspace of $X$ and $S \subseteq Y,$ then $S$ is meager (resp. nonmeager) relative to $Y$ if and only if $S$ is meager (resp. nonmeager) relative to $X.$

Example 3.3: The notion of meager sets plays a critical role ahead, and therefore some examples are in order.

Rationals $\mathbb Q$ and integers $\Z$ are meager in $\mathbb R$ since they can written as a countable union of singletons which are nowhere dense sets in $\mathbb R.$
Every countable set is meager under the setting of Example 2.8.5.
The Cantor set is nowhere dense, and hence also meager. In fact, every nowhere dense in meager.
Any topological space which contains an isolated point $t$ is nonmeager, as no set to which $t$ belongs can be nowhere dense.
We will show in Section 7.3 that the set of functions that have a derivative at some point is a meagre set in the space of real-valued continuous functions on $[0,1]$ endowed with the uniform topology.

Properties Of Meager Sets

Proposition 3.4 (Meager sets form a $\sigma-$ ideal): The collection of meager sets in a topological space

X

form a

\sigma-

ideal.

A subset of a meager set in

X

is again meager in

X

because a subset of a nowhere dense set in

X

is also nowhere dense in

X.

A countable union of meager sets in

X

is again meager in

X

follows from the fact that the Cartesian product of two countable sets is also countable.

It is easily seen that the class of $\mu-$ null sets in a complete measure space $(X, \mathcal{X}, \mu)$ forms a $\sigma-$ ideal, and so does the class of countable subsets of any set $X.$ Therefore, being a $\sigma-$ ideal is a characteristic property of many notions of “smallness” of sets. With that said, these notions of “smallness” may of very different nature as the following theorem shows.

Theorem 3.5 (Oxtoby, 1971): Endow the real line

\mathbb R

with the Lebesgue measure

\lambda.

Then

\mathbb R

can be written as

\mathbb R = A \cup B,

where

A \cap B = \varnothing,

A

is meager in

\mathbb R,

and

\lambda(B) = 0.

Suppose $\{r_n\}_{n \in \mathbb N}$ in an enumeration of the rationals. Consider the family $\left\{I_{n,m}\right\}_{n,m \in \mathbb N}$ of open intervals defined by

I_{n,m} := \left(r_n - \frac{1}{2^{n+m+1}}, r_n + \frac{1}{2^{n+m+1}}\right),

i.e.,

I_{n,m}

is an open interval centered at

r_n

and has Lebesgue measure

1/2^{n+m}.

Also define

G_m := \bigcup_{n \in \mathbb N} I_{n,m}

and

B := \bigcap_{m \in \mathbb N} G_m.

We claim that $\lambda(B) = 0.$ To this end, let $\varepsilon > 0$ be arbitrary. Let $M \in \mathbb N$ be large enough so that $1/2^M < \varepsilon.$ Then since $B \subseteq G_M$ and since

\lambda(G_M) \le \sum_{n \in \mathbb N} \lambda(I_{n,M}) = \sum_{n \in \mathbb N} \frac{1}{2^{n+M}} = \frac{1}{2^M} < \varepsilon,

we have

\lambda(B) < \varepsilon.

Next, we need to show that

A := \mathbb R \setminus B = \bigcup_{m \in \mathbb N} (X \setminus G_m)

is meager in

\mathbb R,

which we can do by showing that

X \setminus G_m

is nowhere dense in

\mathbb R

for each

m \in \mathbb N.

But this is obvious from the definition of

G_m

and from the fact that rationals are dense in

\mathbb R.

It follows from this theorem that every subset of $\mathbb R$ can be partitioned into a meager set and a set of Lebesgue measure $0.$

We next prove the Banach category theorem which says that any topological space is “almost” a Baire space (see the next section for the definition of a Baire space). More specifically, given this theorem, we can write any topological space $X$ as a union of a Baire space (union of all nonmeager open sets) and a meager set (union of all meager open sets) since in a Baire space every nonempty open set is nonmeager.

Theorem 3.6 (Banach Category Theorem): In a topological space

X,

the union of any family of meager open sets is also meager.

Let $\mathcal{U}$ be a family of nonempty meager open subsets of $X,$ and denote by $O = \bigcup_{U \in \mathcal{U}} U$ its union. We want to show that $O$ is meager in $X.$

Let $\mathscr{U}$ denote the set of all collections of pairwise disjoint nonempty open sets in $X$ with the property that each member of each collection is a subset of some member of $\mathcal{U}.$ We will use Zorn's lemma to find a maximal element of $\mathscr{U}.$ $\mathscr{U}$ is partially ordered by set inclusion. Let $\mathscr{C}$ be a chain in $\mathscr{U}.$ To apply Zorn's lemma, we will show that $\mathcal{B} = \bigcup_{\mathcal{R} \in \mathscr{C}} \mathcal{R}$ is an upper bound of $\mathscr{C}$ in $\mathscr{U}$ , i.e., we need to show $\mathcal{B} \in \mathscr{U}$ and $\mathcal{R} \subseteq \mathcal{B}$ for every $\mathcal{R} \in \mathscr{C}.$ But both these claims are immediate from our construction. Therefore, by Zorn's lemma, $\mathscr{U}$ has a maximal element, say $\mathcal{V} = \{V_\alpha \,:\, \alpha \in A\}$ for some index set $A.$ Denote by $V = \bigcup_{\alpha \in A} V_\alpha$ its union.

We next claim that $\mathrm{cl}_X(O) \setminus V$ is nowhere dense in $X.$ Suppose to the contrary that this is not the case, and therefore by Proposition 2.7 (c) there exists a nonempty open subset $W$ of $X,$ such that every nonempty open subset of $W$ intersects $\mathrm{cl}_X(O) \setminus V.$ In particular, $W$ intersects $\mathrm{cl}_X(O) \setminus V,$ which implies $W \cap O \neq \varnothing.$ But then $W \cap U,$ for some $U \in \mathcal{U},$ is a nonempty open set disjoint from all sets in $\mathcal{V},$ contradicting the fact that $\mathcal{V}$ is maximal.

This fact and the fact that $\mathcal{U}$ is a family of meager sets, means that $V_\alpha$ is meager for each $\alpha \in A.$ Write $V_\alpha = \bigcup_{n \in \mathbb N} S_{\alpha, n}$ for some nowhere dense sets $S_{n, \alpha}.$ Define $S_n = \bigcup_{\alpha \in A} S_{\alpha, n}.$ We now claim that $S_n$ is nowhere dense for each ${n \in \mathbb N}.$ To see this suppose $W$ is a nonempty open set in $X$ which intersects $S_n.$ Then $W$ intersects $S_{\alpha, n}$ for some $\alpha \in A,$ and since $S_{\alpha,n}$ is nowhere dense, there exists a nonempty open set $W' \subseteq (W \cap V_\alpha) \setminus S_{\alpha, n}.$ This gives $W' \subseteq W \setminus S_n,$ and thus $S_n$ is nowhere dense.

Finally, note that

O \subseteq \left( \mathrm{cl}_X(O) \setminus V \right) \cup V = \left( \mathrm{cl}_X(O) \setminus V \right) \cup \bigcup_{n \in \mathbb N} S_n,

or in other words, $O$ is a subset of a countable union of nowhere dense sets, which is to say $O$ is meager.

BAIRE SPACES

Definition 4.1 (Baire space): A topological space

X

is said to be a Baire space if every countable union of closed nowhere dense sets in

X

has empty interior in

X.

There are many equivalent formulations for characterizing Baire spaces. Each formulation listed in the next Proposition is more convenient than the other formulations in some proofs, and therefore we will freely use any of them as the definition of a Baire space.

Proposition 4.2 (Equivalent characterizations of Baire space): The following conditions on a topological space $X$ are equivalent:

$X$ is a Baire space.
The intersection of countably many dense open sets in $X$ is dense in $X.$
Each nonempty open subset of $X$ is nonmeager in $X.$
Every meager set in $X$ has empty interior in $X.$
Complements of meager sets in $X$ are dense in $X.$

$(a) \iff (b)$ : If $C$ is a closed nowhere dense subset of $X,$ then by Proposition 2.3 $X \setminus C$ is dense in $X.$ Therefore, taking complement and using Proposition 2.3 we see that countable union of closed nowhere dense sets in $X$ has empty interior if and only if the intersection of countably many dense open sets is dense.

$(c) \implies (a)$ : We will prove the contrapositive, i.e., if there exists a nonempty open subset of $X$ which is meager in $X,$ then there exists a countable collection of closed nowhere dense sets in $X$ such that the interior of their union is nonempty. To that end, let $O = \bigcup_{n \in \mathbb N} S_n$ be a nonempty open subset of $X$ which is meager in $X,$ written as a countable union of nowhere dense sets $\{S_n\}_{n \in \mathbb N}.$ Since closure of closure of a set in simply the closure, the collection $\left\{\mathrm{cl}_X(S_n)\right\}_{n \in \mathbb N}$ is a countable collection of closed nowhere dense sets in $X.$ Therefore, the fact that $O$ is nonempty and the following observation finishes the proof:

O = \mathrm{int}_X(O) = \mathrm{int}_X\left(\bigcup_{n \in \mathbb N} S_n\right) \subseteq \mathrm{int}_X\left(\bigcup_{n \in \mathbb N} \mathrm{cl}_X(S_n)\right).

$(a) \implies (c)$ : We will again prove the contrapositive, i.e., if there exists a countable collection $\{F_n\}_{n \in \mathbb N}$ of closed nowhere dense sets in $X$ such that the interior of their union is nonempty, then there exists a nonempty open subset of $X$ which is meager in $X.$ Denote the nonempty interior $\mathrm{int}_X\left(\bigcup_n F_n\right)$ by $O.$ Consider the countable collection $\{F_n \cap O\}_{n \in \mathbb N}$ and note that since a subset of a nowhere dense set is also nowhere dense, the collection consists of nowhere dense sets in $X.$ The set $O$ is a subset of $\bigcup_n F_n$ and therefore

O = O \cap \bigcup_{n \in \mathbb N} F_n = \bigcup_{n \in \mathbb N} (F_n \cap O),

showing that

O

is meager in

X.

$(c) \iff (d)$ : Follows immediately from the observation that a subset of a meager set in $X$ is also meager in $X.$

Example 4.3:

Trivially, singleton sets are always Baire spaces.
Baire category theorems, proved in Section 5 provide the most common examples of Baire spaces, namely, locally compact Hausdorff spaces and complete pseudo-metric spaces. In particular, the Euclidean spaces $\mathbb R^n$ for all $n \in \mathbb N$ are Baire spaces.
The space $\mathbb Q$ of rationals (with the subspace topology as a subspace of $\mathbb R$ ) is not a Baire space. Indeed, singletons in $\mathbb Q$ are closed and have empty interior, and therefore $\mathbb Q,$ which can be written as a countable union of all its singletons, cannot be Baire.
The space $\mathbb R \setminus \mathbb Q$ of irrationals (with the subspace topology as a subspace of $\mathbb R$ ) is a Baire space.
The space $\mathbb N$ of natural numbers (with the subspace topology as a subspace of $\mathbb R$ ) is a Baire space.

Properties Of Baire Spaces

Consider the Baire space $\mathbb R^2 \setminus \left(\left(\mathbb R \setminus \mathbb{Q}\right) \times \{0\}\right).$ Its closed subset $\mathbb{Q} \times \{0\}$ is clearly meager. Therefore, a subspace of a Baire space may not be Baire. But if the subspace is open then it is Baire.

Proposition 4.4 (Open Subspaces of Baire are Baire): If

X

is a Baire space and

Y \subseteq X

is open, then

Y

is also a Baire space.

Let $\{S_n\}_{n \in \mathbb N}$ be a countable collection of closed nowhere dense sets in $Y.$ We need to show that $\bigcup_{n \in \mathbb N} S_n$ has empty interior in $Y.$ Since $S_n$ is closed in $Y,$ we have $\mathrm{cl}_X(S_n) \cap Y = S_n$ for each $n \in \mathbb N.$ We claim that $\mathrm{cl}_X(S_n)$ is nowhere dense in $X$ for each $n \in \mathbb N.$

To see this, suppose to the contrary that there exists a nonempty open subset $U$ of $X$ such that $U \subseteq \mathrm{cl}_X(S_n).$ Then $U$ must intersect $S_n.$ Therefore, $U \cap Y$ is a nonempty open subset of $Y$ contained in $S_n.$ This contradicts the fact that $S_n$ is nowhere dense in $Y.$

We can now use the fact that $X$ is a Baire space and get that $\bigcup_{n \in \mathbb N} \mathrm{cl}_X(S_n)$ has empty interior. Now note that if $\bigcup_{n \in \mathbb N} S_n$ didn't have empty interior in $Y,$ then there would exist a nonempty open subset $V$ of $Y$ such that $V \subseteq \bigcup_{n \in \mathbb N} S_n.$ This set $V$ is also open in $X$ because $Y$ is an open subset of $X,$ and then $V \subseteq \bigcup_{n \in \mathbb N} \mathrm{cl}_X(S_n)$ would give a contradiction.

For another proof recall Remark 3.2 and the characterization from Proposition 4.2 (c) of Baire spaces, and then use the fact that an open subset of $Y$ is also an open subset of $X.$

Even a dense subspace of a Baire space may not be Baire as is verified by the fact that $\mathbb{Q}$ is not a Baire space but is a dense subspace of the Baire space $\mathbb R.$ However, a dense $G_\delta-$ subspace of a Baire space is a Baire space. See Proposition 1.23 in (Haworth and McCoy, 1977) for a proof.

The next proposition will useful is showing that $\mathbb{Q}$ is not homeomorphic to any complete metric space in Section 7.1.

Proposition 4.5 (Preservation under homeomorphism): If two topological spaces

X

and

Y

are homeomorphic, and

X

is a Baire space, then so is

Y.

The proof is trivial since being an open subset and being a dense subset are both invariant under homeomorphisms, and since homeomorphisms are bijections, the image of the intersection is the intersection of the images.

Proposition 4.6 (Closure Of Baire Subspace is Baire): Let

Y

be a dense subset of a topological space

X

such that it is Baire. Then

X

is also a Baire space.

Suppose to the contrary

X

is not a Baire space. Then by Proposition 4.2 (c) there exists a nonempty open meager subset

U

X.

But then

Y \cap U

is a nonempty open meager subset of

Y

by Proposition 3.4, which contradicts the fact that

Y

is a Baire space.

For a topological space $X,$ an arbitrary union of Baire subspaces of $X$ need not be Baire since a singleton set is a Baire space. But we have the following two results if the Baire subspaces are open or if the union is of a finite family.

Proposition 4.7 (Arbitrary Union of Open Baire Spaces): In a topological space

X,

the union of any family of open Baire subspaces is a Baire space.

Let

\mathcal{U}

be a family of open Baire subspaces of

X.

Suppose

V

is an open meager subset of

\bigcup_{U \in \mathcal{U}} U.

Let

U \in \mathcal{U}

be such that it intersects

V.

Then

U \cap V

is open and meager in

U.

Therefore, by Proposition 4.2 (e),

\bigcup_{U \in \mathcal{U}} U

is Baire since

U

is Baire.

Proposition 4.8 (Finite Union of Baire Spaces): In a topological space

X,

the union of a finite family of Baire subspaces is a Baire space.

It is sufficient to show the proposition for two Baire subspaces. Without loss of generality, we can let $X = Y \cup Z,$ where $Y$ and $Z$ are Baire spaces, and we want to show that $X$ is a Baire space.

$X \setminus \mathrm{cl}_X(Y)$ and $X \setminus \mathrm{cl}_X(Z)$ are open in $Z$ and $Y,$ respectively, and hence by Proposition 4.4, they both Baire spaces. By Proposition 4.7 then

B = \left(X \setminus \mathrm{cl}_X(Y)\right) \cup \left(X \setminus \mathrm{cl}_X(Z)\right) = X \setminus \left(\mathrm{cl}_X(Y) \cap \mathrm{cl}_X(Z)\right)

is an open Baire subspace of

X.

By Proposition 4.6,

\mathrm{cl}_X(Y)

is a Baire space, and since

X \setminus \mathrm{cl}_X(B)

is its open subset, by Proposition 4.4,

X \setminus \mathrm{cl}_X(B)

is a Baire space. But

B \cup \left(X \setminus \mathrm{cl}_X(B)\right)

is a Baire subspace by Proposition 4.7 and is dense in

X,

and therefore by Proposition 4.6,

X

is Baire.

Products of Baire spaces may not be Baire space. The analysis is involved. See (Cohen, 1976) for details.

As is intuitively expected, a disjoint sum of Baire spaces is Baire.

Proposition 4.9 (Disjoint sums): Every disjoint topological sum of Baire spaces is a Baire space.

For Baire spaces

\{X_\alpha\}_{\alpha \in A},

let

X = \bigsqcup_{\alpha \in A} X_\alpha

be their disjoint sum and let

U

be an open subset of

X.

By Proposition 4.4,

U \cap X_\alpha

is a Baire space if the intersection is nonempty. Since

U = \bigcup_{\alpha} (U \cap X_\alpha),

where the union is over all such

\alpha,

by Proposition 4.7,

U

is a Baire space.

X

can now be written as a union of open Baire spaces and hence is Baire.

The last property we consider is the relation of being Baire with the underlying topology. Suppose $(X, \mathcal T)$ is a topological space. Then $(X, 2^X)$ is always a Baire space since it can be completely metrized using the discrete metric

\begin{aligned} d(x,y) =\begin{cases}1 &\text{if } x \neq y \\0 &\text{if } x = y\end{cases}, \quad x,y \in X.\end{aligned}

Therefore, even if

(X, \mathcal{T})

is a Baire space,

(X, \mathcal{S})

may not be a Baire space if

\mathcal{S}

is strictly coarser than

\mathcal{T}.

BAIRE CATEGORY THEOREMS

In this section we prove the main results of this blog post, the Baire category theorems. They state that if $X$ is a locally compact Hausdorff space or a complete pseudometric space, then $X$ is a Baire space. These theorems will have many applications as we will see in Section 7. Proving both these results involves constructing a nested sequence of open sets and then showing that the intersection of their closures is nonempty. We start with proving the Baire category theorem for locally compact Hausdorff spaces, for which we will need a few results which we prove next.

Since locally compact spaces have different meanings in literature, let us define it for our use case.

Definition 5.1 (Locally compact): A topological space

X

is said to be locally compact at $x \in X$ if there is some compact subspace

C \subseteq X

that contains a neighborhood of

x.

X

is locally compact at each of its points,

X

is said to be locally compact.

The first result we need is an equivalent characterization of locally compact Hausdorff spaces. This characterization will allow us to construct our nested sequence of open sets. But even before that we need a simple lemma.

Lemma 5.2 (A point outside a compact subspace in a Hausdorff space can be separated): If

Y

is a compact subspace of a Hausdorff space

X

and

x \in X \setminus Y,

then there exist disjoint open subsets

U

and

V

X

such that

x \in U

and

Y \subseteq V.

For each

y \in Y,

there exists a pair of disjoint open sets

(U_y, V_y)

such that

x \in U_y

and

y \in V_y,

because

X

is Hausdorff. By our construction, the collection

\{V_y\}_{y \in Y}

is an open cover for the compact set

Y,

and therefore, there exists a finite subcover, say

\{V_i\}_{i=1}^n.

Define

V = \bigcup_{i=1}^n V_i

and define

U = \bigcap_{i=1}^n U_i,

giving us the desired disjoint open sets.

Proposition 5.3 (Equivalent characterization of local compactness in Hausdorff spaces): Let

X

be a Hausdorff space. Then

X

is locally compact if and only if given an open subset

U \subseteq X

and a point

x \in U,

there is an open subset

V \subseteq X

containing

x

such that

\mathrm{cl}_X(V)

is compact and

\mathrm{cl}_X(V) \subseteq U.

The if side is easy: Given a point $x \in X$ and letting $U=X$ in the hypothesis, there is an open subset $V \subseteq X$ containing $x$ such that $\mathrm{cl}_X(V)$ is compact, and therefore $\mathrm{cl}_X(V)$ serves as the compact set containing the neighborhood $V$ of $x.$

For the other side, suppose $X$ is a locally compact Hausdorff space, and let $U$ be an open set in $X$ with $x \in U.$ Let $X^*$ be the Alexandroff one-point compactification of $X.$ Then since $U$ is open in $X,$ it is also open in $X^*,$ and thus $X^* \setminus U$ is closed in $X^*.$ Since $X^*$ is compact, $X^* \setminus U$ is a compact subspace of $X^*.$ Since $X^*$ is Hausdorff, we can use Lemma 5.2 to find disjoint open subsets $V$ and $W$ of $X^*$ such that $x \in V$ and $X^* \setminus U \subseteq W.$ The closure $\mathrm{cl}_{X^*}(V)$ is compact and satisfies $\mathrm{cl}_{X^*}(V) \cap (X^* \setminus U) = \varnothing.$ Therefore, $\mathrm{cl}_{X^*}(V) = \mathrm{cl}_X(V)$ is compact and satisfies $\mathrm{cl}_X(V) \subseteq U,$ as desired.

We next prove a proposition that allows us to make claims about the non-emptiness of intersection of a family of closed sets satisfying the finite intersection property. Recall that a collection $\mathcal{C}$ of subsets of $X$ is said to have the finite intersection property if every finite subcollection of $\mathcal{C}$ has nonempty intersection.

Proposition 5.4 (Equivalent characterization of compactness): A topological space

X

is compact if and only if for every collection

\mathcal{C}

of closed sets in

X

having the finite intersection property, the intersection

\bigcap_{C \in \mathcal{C}} C

is nonempty.

$X$ is compact means that given any collection $\mathcal{U}$ of open sets, if no finite subcollection covers $X,$ then $\mathcal{U}$ cannot cover $X.$ Define the collection $\mathcal{C} = \{X \setminus U \,:\, U \in \mathcal{U}\}$ of closed sets in $X,$ and note that we could have constructed $\mathcal{U}$ given $\mathcal{C}$ similarly. It is easy to see that the collection $\mathcal{U}$ does not cover $X$ if and only if $\bigcap_{C \in \mathcal{C}} C$ is nonempty, and similarly a finite subcollection $\{U_1, \ldots, U_n\}$ of $\mathcal{U}$ does not cover $X$ if and only if the intersection $\bigcap_{i=1}^n C_i$ of the corresponding closed sets from $\mathcal{C}$ is nonempty.

Therefore, the statement “given any collection $\mathcal{U}$ of open sets, if no finite subcollection covers $X,$ then $\mathcal{U}$ cannot cover $X$ ”, is equivalent to the statement “given any collection $\mathcal{C}$ of closed sets, if every finite intersection of elements of $\mathcal{C}$ is nonempty, then the intersection $\bigcap_{C \in \mathcal{C}} C$ is nonempty”.

We have now done most of the legwork to establish the Baire category theorem for locally compact Hausdorff spaces.

Theorem 5.5 (Baire category theorem for locally compact Hausdorff space): Every locally compact Hausdorff space

X

is a Baire space.

Let $\{U_n\}_{n \in \mathbb N}$ be a collection of dense open sets in $X.$ We want to show that their intersection is also dense in $X,$ i.e., we want to show that for any nonempty open subset $V \subseteq X,$ the intersection

\begin{aligned} V \cap \left( \bigcap_{n \in \mathbb N} U_n \right)\end{aligned}

is nonempty. To that end, fix an arbitrary nonempty open subset

V \subseteq X.

Since

U_1

is dense in

X,

there exists a point

x_1 \in V \cap U_1.

Proposition 5.3 implies that there exists an open subset

V_1 \subseteq X

containing

x_1

such that

\mathrm{cl}_X(V_1)

is compact and

\mathrm{cl}_X(V_1) \subseteq V \cap U_1.

Similarly, for

n > 1,

we use Proposition 5.3 to get a nonempty open subset

V_n \subseteq X

such that

\mathrm{cl}_X(V_n)

is compact and

\mathrm{cl}_X(V_n) \subseteq V_{n-1} \cap U_n.

The sequence $\mathrm{cl}_X(V_1) \supseteq \mathrm{cl}_X(V_2) \supseteq \cdots$ is a collection of closed sets in the compact space $\mathrm{cl}_X(V_1)$ satisfying the finite intersection property, and therefore by Proposition 5.4, the intersection $\bigcap_{n \in \mathbb N} \mathrm{cl}_X(V_n)$ is nonempty. But note that by our construction

\begin{aligned} \bigcap_{n \in \mathbb N} \mathrm{cl}_X(V_n) \subseteq V \cap \left( \bigcap_{n \in \mathbb N} U_n \right),\end{aligned}

showing that

V \cap \left( \bigcap_{n \in \mathbb N} U_n \right)

is nonempty.

The proof of Baire category theorem for complete pseudometric space proceeds in a very similar fashion, except here we use completeness instead of compactness to show that the intersection of the closures of the sequence of open sets constructed is nonempty. Recall that, unlike metric spaces, in a pseudometric space it is possible for the distance between two distinct points to be $0.$

Theorem 5.6 (Baire category theorem for complete pseudometric space): Every complete metric space

(X,d)

is a Baire space.

$(X, d)$ is equipped with the pseudometric topology generated by the open balls

\begin{aligned} B_r(p) = \{x \in X \,:\, d(x,p) < r\}, \quad p \in X,\, r > 0,\end{aligned}

which form a basis for the topology. For any subset

A

X,

denote by

\begin{aligned} d(A) = \sup \{d(s,t) \,:\, s,t \in A\}\end{aligned}

the diameter of

A,

and define

d^*(A) := \min \{1, d(A)\}.

Observe that if

A \subseteq B \subseteq X

then

d^*(A) \le d^*(B).

\begin{aligned} V \cap \left( \bigcap_{n \in \mathbb N} U_n \right)\end{aligned}

is nonempty. To that end, fix an arbitrary nonempty open subset

V \subseteq X.

Since

U_1

is dense in

X,

there exists a point

x_1 \in V \cap U_1.

By the definition of a basis, we can choose

r \in (0,1)

such that

B_r(x_1) \subseteq V \cap U_1.

If we define

r' := d(B_r(x_1)),

then by triangle inequality

r'/2 \le r < 1.

Thus if we define

V_1 = B_{r'/4}(x_1)

we have

\begin{aligned} \mathrm{cl}_X(V_1) \subseteq \left\{x \in X \,:\, d(x,x_1) \le \frac{r'}{4}\right\} \subseteq B_r(x_1) \subseteq V \cap U_1,\end{aligned}

and by triangle inequality

\begin{aligned} d(V_1) \le \frac{r'}{2} = \frac{d^*(B_r(p))}{2} \le \frac{d^*(V \cap U_1)}{2} \le \frac{d(V \cap U_1)}{ 2}.\end{aligned}

Similarly, for

n > 1,

we construct a nonempty open subset

V_n \subseteq X

such that

\begin{aligned} \mathrm{cl}_X(V_n) \subseteq V_{n-1} \cap U_n\end{aligned}

and

\begin{aligned} d(V_n) \le \frac{d^*(V_{n-1}) }{ 2} \le \frac{d(V_{n-1}) }{ 2}.\end{aligned}

We claim that $\bigcap_{n \in \mathbb N} \mathrm{cl}_X(V_n)$ is nonempty. Since $d^*(V_1) \le 1$ and $d(V_{n+1}) \le d^*(V_n) / 2,$ we have $d(V_{n}) \le 2^{-n+1}$ for each $n \in \mathbb N.$ Each of these sets is nonempty and therefore we can choose $x_n \in V_n$ for each ${n \in \mathbb N}.$ The sequence $\{x_n\}_{n \in \mathbb N}$ becomes a Cauchy sequence and therefore since $X$ is complete there exists $x \in X$ such that it is the limit of this sequence. By our construction, if $m \le n,$ then $x_n \in V_m \subseteq \mathrm{cl}_X(V_m).$ Thus, $x \in \mathrm{cl}_X(V_n)$ for each ${n \in \mathbb N}.$ This shows that $x \in \bigcap_n \mathrm{cl}_X(V_n).$

But note that by our construction

\begin{aligned} \bigcap_{n \in \mathbb N} \mathrm{cl}_X(V_n) \subseteq V \cap \left( \bigcap_{n \in \mathbb N} U_n \right),\end{aligned}

showing that

V \cap \left( \bigcap_{n \in \mathbb N} U_n \right)

is nonempty.

As a trivial (but useful!) corollary a complete metric space is a Baire space.

Locally compact Hausdorff spaces and completely metrizable spaces are of very different nature, and therefore it is surprising that they both are Baire spaces and in this sense have many common properties. As an example of a locally compact Hausdorff that isn't a complete metric space, consider $[0,1]^J$ for uncountable set $J$ or $(0,1)$ with the subspace topology with respect to $\mathbb R.$ In fact, $[0,1]^J$ is a compact Hausdorff space that isn't even metrizable. On the other hand, $\mathbb N^\mathbb N$ (which is homeomorphic to the space of irrationals) and infinite-dimensional Hilbert spaces are examples of complete metric spaces that aren't locally compact Hausdorff. Finally, the Sorgenfrey plane and the Niemytzki/Moore plane are Baire spaces which are neither complete pseudometric spaces nor a locally compact Hausdorff spaces.

TOPOLOGICAL GAMES

A topological game is typically a 2-player game where the two players choose some objects related to the topological structure of a space, such as points, closed subsets, open covers, etc., in each round of the game with a goal in mind. The conditions on a play to be winning for a player also involves topological notions such as closure, a convergence, etc. Remarkably, it turns out that topological games can be used to define notions such as Baire property, Baire spaces, completeness properties, convergence properties, separation properties, continuous images, Suslin sets, etc. Viewing these topological notions through the lens of topological games often provides more insight and is even sometimes a more natural perspective.

In this section we will discuss two 2-player games, Banach-Mazur game and Choquet game. These games are closely tied to meager sets and Baire spaces.

In the period 1930s and 1940s mathematicians from the Lwów school in Poland, which included Banach, Ulam, Kuratowski, Steinhaus, Mazur, Kac, Alexandroff, von Neumann, Orlicz, Sobolev, Borsuk, Zygmund, Schauder, Eilenberg among others, collaboratively discussed problems, mainly in topology and functional analysis. In 1935, Banach started a famous notebook, called the Scottish Book, where these mathematicians proposed mathematical conjectures. In the same year Mazur proposed a topological game related to the Baire category theorem. A solution was proposed by Banach and therefore the game is now known as Banach-Mazur game (Telegarsky, 1987). It was the first infinite positional game of perfect information to be studied.

Banach-Mazur Game

Let us state and prove the Banach-Mazur game as it proposed originally by Mazur. Instead of general topological spaces $X$ we will be limiting ourselves to sets on the real line equipped with the usual Euclidean topology. We use the phrase closed interval to refer to intervals of the form $[a,b]$ for $a < b$ .

Definition 6.1 (Banach-Mazur Game): Player

\mathcal P_{A}

is dealt an arbitrary subset

A

of a closed interval

I_0

. The complement

B = I_0 \setminus A

is dealt to the player

\mathcal P_{B}

. The game, denoted by

\mathrm{BM}\!\left( A, B\right)

, is played as follows:

\mathcal P_{A}

chooses any closed sub-interval

I_1 \subseteq I_0

; then

\mathcal P_{B}

chooses any closed sub-interval

I_2 \subseteq I_1

; and so on, alternatively. Together the players determine a nested sequence

I_0 \subseteq I_1 \subseteq I_2 \subseteq \cdots

of closed intervals,

\mathcal P_{A}

choosing those with odd index and

\mathcal P_{B}

choosing those with even index.

\mathcal P_{A}

wins if and only if

A \cap \left( \bigcap_{n \in \mathbb N} I_n \right) \neq \varnothing

; otherwise,

\mathcal P_{B}

wins.

The following theorem due to Mazur states that if $A$ is meager then there exists a strategy which $\mathcal P_{B}$ can use to win the game no matter what $\mathcal P_{A}$ plays.

Theorem 6.2: If

I_0

is any closed interval and

A \cup B

a partition of

I_0

, then there exists a winning strategy for

\mathcal P_{B}

for the game

\mathrm{BM}\!\left( A, B\right)

A

is meager in

I_0

Write

A = \bigcup_{n \in \mathbb N} A_n

as a countable union of nowhere dense sets in

I_0

. Then at each step

{n \in \mathbb N}

\mathcal P_{B}

can choose a closed interval

I_{2n}

such that

I_{2n} \subseteq I_{2n-1} \setminus A_n

. Then

A \cap \left( \bigcap_{n \in \mathbb N} I_{2n} \right) = \varnothing

, and therefore no matter how

\mathcal P_{A}

plays,

\mathcal P_{B}

will win.

Mazur conjectured that only when $A$ is meager in $I_0$ does there exist a strategy which $\mathcal P_{B}$ can use to win. Banach proved this result. Before we give the proof, let us formalize what we mean by a "strategy".

Definition 6.3 (Strategy): A strategy for either player is a sequence of closed-interval-valued functions each of which specify the choice of the set by the player in the corresponding move while satisfying the rules of the game. More specifically, for

\mathcal P_{B}

denote the strategy by the sequence

\left\{ f_n\right\}_{n \in \mathbb N}

such that for each

{n \in \mathbb N}

\begin{aligned} I_{2n} = f_n(I_0, I_1, \ldots, I_{2n-1}) \subseteq I_{2n-1}.\end{aligned}

Then this is a winning strategy for

\mathcal P_{B}

if and only if

\bigcap_{n \in \mathbb N} I_n \subseteq B

for any valid choice of

\left\{ I_{2n-1}\right\}_{n \in \mathbb N}

\mathcal P_{A}

Theorem 6.4: If

I_0

is any closed interval and

A \cup B

a partition of

I_0

, then there exists a winning strategy for

\mathcal P_{B}

for the game

\mathrm{BM}\!\left( A, B\right)

if and only if

A

is meager in

I_0

We have already proved the if part in Theorem 6.2. So assume that $\left\{ f_n\right\}_{n \in \mathbb N}$ is a winning strategy for $\mathcal P_{B}$ . We want to show that $A$ is meager, which we do by showing that $A$ is a subset of a countable union $\bigcup_{n \in \mathbb N} (I_0 \setminus G_n)$ of nowhere dense sets. This we will do by constructing open sets $\left\{ G_n\right\}_{n \in \mathbb N}$ such that each $G_n$ is dense in $I_0$ . The construction proceeds by induction to first construct clever families of sets $\left\{ J_{i_1, \ldots, i_n} \,:\, n, i_1, \ldots, i_n \in \mathbb N\right\}$ and $\left\{ K_{i_1, \ldots, i_n} \,:\, n, i_1, \ldots, i_n \in \mathbb N\right\}$ which are used to define $\left\{ G_n\right\}_{n \in \mathbb N}$ and also a particular sequence $\left\{ I_n\right\}_{n \in \mathbb N}$ for which, since $\left\{ f_n\right\}_{n \in \mathbb N}$ is a winning strategy, we will use the fact that $\bigcap_{n \in \mathbb N} I_n \subseteq B$ . To that end let us start by constructing the families $\left\{ J_{i_1, \ldots, i_n} \,:\, n, i_1, \ldots, i_n \in \mathbb N\right\}$ and $\left\{ K_{i_1, \ldots, i_n} \,:\, n, i_1, \ldots, i_n \in \mathbb N\right\}$ .

The collection $\mathcal S$ of all closed intervals that have rational endpoints and are contained in $\mathrm{int}_{ \mathbb R}\!\left( I_0\right)$ is countable and therefore $\mathcal S$ can be thought of as a sequence. We define two sequences $\left\{ J_n\right\}_{n \in \mathbb N}$ and $\left\{ K_n = f_1(I_0, J_n)\right\}_{n \in \mathbb N}$ of closed intervals as follows: $J_1$ is the first element of $\mathcal S$ ; for $n > 1$ , define $J_n$ to be the first term of $\mathcal S$ contained in $I_0 \setminus \left( \bigcup_{i=1}^{n-1}K_i \right)$ . We then have

(i) for each ${n \in \mathbb N}$ , $J_n\subseteq\mathrm{int}_{ \mathbb R}\!\left( I_0\right)$ ,

(ii) the sets $\left\{ K_n\right\}_{n \in \mathbb N}$ are pairwise disjoint, and

(iii) $\bigcup_{n \in \mathbb N} \mathrm{int}_{ \mathbb R}\!\left( K_n\right)$ is dense in $I_0$ .

The first and the second property are obvious from the construction and the fact that $K_n \subseteq f_1(I_0, J_n)$ . The third property follows from the fact that rationals are dense in $\mathbb R$ , and therefore for every open subset of $I_0$ we can find a closed interval with rational endpoints lying inside this open set. Note that the elements of the sequence $\left\{ J_n\right\}_{n \in \mathbb N}$ are contained in $\mathrm{int}_{ \mathbb R}\!\left( I_0\right)$ .

Similarly, for each $m \in \mathbb N$ , let $\left\{ J_{m,n}\right\}_{n \in \mathbb N}$ be a sequence of closed intervals contained in $\mathrm{int}_{ \mathbb R}\!\left( K_m\right)$ such that the sets $\left\{ K_{m,n} = f_2(I_0, J_m, K_m, J_{m,n})\right\}_{n \in \mathbb N}$ are pairwise disjoint, and $\bigcup_{n \in \mathbb N} \mathrm{int}_{ \mathbb R}\!\left( K_{m,n}\right)$ is dense in $K_m$ . Now recall Proposition 2.6, which implies that $\bigcup_{m,n \in \mathbb N} \mathrm{int}_{ \mathbb R}\!\left( K_{m,n}\right)$ is dense in $I_0$ .

Proceeding inductively, we define two families of closed intervals

\begin{gathered} \left\{ J_{i_1, \ldots, i_n} \,:\, n, i_1, \ldots, i_n \in \mathbb N\right\} \text{, and} \\ \left\{ K_{i_1, \ldots, i_n} = f_n(I_0, J_{i_1}, K_{i_1}, J_{i_1, i_2}, K_{i_1, i_2}, \ldots, J_{i_1, \ldots, i_n}) \,:\, n, i_1, \ldots, i_n \in \mathbb N\right\} \end{gathered}

satisfying the following properties

(i) $J_{i_1, \ldots, i_n} \subseteq \mathrm{int}_{ \mathbb R}\!\left( K_{i_1, \ldots, i_n}\right)$ ,

(ii) for each ${n \in \mathbb N}$ , the sets $\left\{ K_{i_1, \ldots, i_n} \,:\, i_1, \ldots, i_n \in \mathbb N\right\}$ are pairwise disjoint, and

(iii) for each ${n \in \mathbb N}$ , $\bigcup_{i_1, \ldots, i_n \in \mathbb N} \mathrm{int}_{ \mathbb R}\!\left( K_{i_1, \ldots, i_n}\right)$ is dense in $I_0$ .

Having defined these families, note that if $\left\{ i_n\right\}_{n \in \mathbb N}$ is any arbitrary sequence of positive integers, then the sequence $\left\{ I_n\right\}_{n \in \mathbb N}$ such that $\begin{aligned} I_{2n-1} = J_{i_1, \ldots, i_n} \text{ and } I_{2n} = K_{i_1, \ldots, i_n}, \quad {n \in \mathbb N}\end{aligned}$ is a valid play of the game consistent with the strategy $\left\{ f_n\right\}_{n \in \mathbb N}$ of $\mathcal P_{B}$ . By hypothesis, $\left\{ f_n\right\}_{n \in \mathbb N}$ is a winning strategy, and therefore $\bigcap_{n \in \mathbb N} I_n \subseteq B$ .

Define the sequence $\left\{ G_n\right\}_{n \in \mathbb N}$ of open sets by

\begin{aligned} G_n = \bigcup_{i_1, \ldots, i_n \in \mathbb N} \mathrm{int}_{ \mathbb R}\!\left( K_{i_1, \ldots, i_n}\right),\end{aligned}

and let

E = \bigcap_{n \in \mathbb N} G_n

be their intersection. Then

E \subseteq B

because if

x \in E

, then

x

is in every

G_n

, which with property (ii) gives a unique sequence

\left\{ i_n\right\}_{n \in \mathbb N}

such that

x \in K_{i_1, \ldots, i_n}

for every

{n \in \mathbb N}

, which if used to define

\left\{ I_n\right\}_{n \in \mathbb N}

like in (2) and noting

K_{i_1, \ldots, i_n} \subseteq J_{i_1, \ldots, i_n}

gives

x \in \bigcap_{n \in \mathbb N} I_n \subseteq B

. But now note that

\begin{aligned} A = I_0 \setminus B \subseteq I_0 \setminus E = \bigcup_{n \in \mathbb N} (I_0 \setminus G_n).\end{aligned}

By the definition of

G_n

and property (iii),

I_0 \setminus G_n

is nowhere dense in

I_0

for each

{n \in \mathbb N}

. This finishes the proof.

This theorem gives new insight into the sense in which a meager set is "small" - even the advantage of being the first player is not enough. When can the player $\mathcal P_{A}$ be sure to win? This is answered by the next theorem, and is a simple consequence of our previous theorem.

Theorem 6.5: If

I_0

is any closed interval and

A \cup B

a partition of

I_0

, then there exists a winning strategy for

\mathcal P_{A}

for the game

\mathrm{BM}\!\left( A, B\right)

if and only if

B

is meager in some closed interval

I_1 \subseteq I_0

If such a closed interval $I_1$ exists, then $\mathcal P_{A}$ can start by choosing $I_1$ and then by following the strategy of $\mathcal P_{B}$ in Theorem 6.2, $\mathcal P_{A}$ can ensure than $B \cap \left( \bigcap_{n \in \mathbb N} I_n \right) = \varnothing$ . The intersection $\bigcap_{n \in \mathbb N} I_n$ is nonempty (see the proof of Theorem 5.6 where a generalization of this well-known fact was proved), and therefore this is a winning strategy for $\mathcal P_{A}$ .

On the other hand, if $\mathcal P_{A}$ has a winning strategy, then suppose he chooses $I_1$ as his first move. After this move, the game $\mathrm{BM}\!\left( A, B\right)$ becomes the game $\mathrm{BM}\!\left( I_1 \cap B, I_1 \cap A\right)$ and player $\mathcal P_{A}$ becomes player $\mathcal P_{I_1 \cap A}$ . Then using Theorem 6.4 $\mathcal P_{I_1 \cap A}$ has a winning strategy only if $I_1 \cap B$ is meager in $I_1$ .

Is it possible that neither player has a winning strategy? Yes, for example, if $A = I_0 \cap B$ , where $B$ is the Bernstein set, which is defined to be a subset of $\mathbb R$ such that both $B$ and $\mathbb R \setminus B$ intersect every uncountable closed set. For a proof of this result, see Chapter-6 in (Oxtoby, 1971).

Generalization

In (Oxtoby, 1957), Oxtoby proved a generalization of the above game. The game is still called the Banach-Mazur game. We will not be proving this result, but will state it for completeness.

Definition 6.6 (Banach-Mazur Game): Let $X$ be any topological space, and let $\mathcal G$ be a specified class of subsets of $X$ such that

(i) each element of $\mathcal G$ has a nonempty interior in $X$ , and

(ii) every nonempty open subset of $X$ contains an element of $\mathcal G$ .

Let $X = A \cup B$ be an arbitrary partition of $X$ . The game $\mathrm{BM}\!\left( A, B\right)$ is played by two players $\mathcal P_{A}$ and $\mathcal P_{B}$ as follows: $\mathcal P_{A}$ chooses any $G_1 \in \mathcal G$ ; then $\mathcal P_{B}$ chooses any $G_2 \in \mathcal G$ such that $G_2 \subseteq G_1$ ; and so on alternatively. Together the players determine a nested sequence $G_1 \subseteq G_2 \subseteq \cdots$ of elements from $\mathcal G$ , with $\mathcal P_{A}$ choosing those with odd index and $\mathcal P_{B}$ choosing those with even index.

$\mathcal P_{A}$ wins if and only if $A \cap \left( \bigcap_{n \in \mathbb N} G_n \right) \neq \varnothing$ ; otherwise $\mathcal P_{B}$ wins.

Theorem 6.7 ((Oxtoby, 1957)): (i) Using the notion above, there exists a winning strategy for $\mathcal P_{B}$ for the game $\mathrm{BM}\!\left( A, B\right)$ if and only if $A$ is meager in $X$ .

(ii) If we assume that $X$ is a complete metric space, there exists a winning strategy for $\mathcal P_{A}$ for the game $\mathrm{BM}\!\left( A, B\right)$ if and only if $B$ is meager in some nonempty open subset of $X$ .

The proof is very similar to the proof of the Theorems 6.4 and 6.5. For details see (Oxtoby, 1957).

Choquet Game

Choquet game proposed by Choquet in his book (Choquet, 1969) is closely related to the Banach-Mazur game.

Definition 6.8 (Choquet Game): Let $X$ be a nonempty topological space. The _Choquet game} $C_X$ of $X$ is a game with two players $\mathcal P_X$ and $\mathcal P_\varnothing$ taking turns in choosing nonempty open subsets of $X$ as follows: Player $\mathcal P_X$ chooses $G_1$ , then player $\mathcal P_\varnothing$ chooses $G_2 \subseteq G_1$ ; and so on alternatively. Together the players determine a nested sequence $G_1 \subseteq G_2 \subseteq \cdots$ of nonempty open subsets of $X$ , with $\mathcal P_X$ choosing those with odd index and $\mathcal P_\varnothing$ choosing those with even index.

$\mathcal P_\varnothing$ wins this game if and only if $\bigcap_{n \in \mathbb N} G_n \neq \varnothing$ ; otherwise $\mathcal P_X$ wins.

Note the similarity between this game and the Banach-Mazur game specified by taking $A = X$ and $\mathcal G$ to be the collection of all nonempty open subsets of $X$ in Definition 6.6. In the Banach-Mazur game we say $\mathcal P_X$ wins $\mathrm{BM}\!\left( X, \varnothing\right)$ if and only if $\bigcap_{n \in \mathbb N} G_n \neq \varnothing$ , while in the Choquet game we say $\mathcal P_\varnothing$ wins $C_X$ if and only if $\bigcap_{n \in \mathbb N} G_n \neq \varnothing$ . This swap changes a lot though as the following theorem demonstrates.

Theorem 6.9: A nonempty topological space

X

is a Baire space if and only if player

\mathcal P_X

has no winning strategy in the Choquet game

C_X

Having shown the relation between the Choquet and Banach-Mazur games, let us change the notation a little for convenience. Let us denote the players $\mathcal P_X$ and $\mathcal P_\varnothing$ by $\mathcal P_1$ and $\mathcal P_2$ respectively for players $1$ and $2$ . The choices of $\mathcal P_1$ which is the collection $\left\{ G_{2n-1}\right\}_{n \in \mathbb N}$ is denoted by $\left\{ U_n\right\}_{n \in \mathbb N}$ and the choices of $\mathcal P_2$ which is the collection $\left\{ G_{2n}\right\}_{n \in \mathbb N}$ is denoted by $\left\{ V_n\right\}_{n \in \mathbb N}$ . The strategy for $\mathcal P_1$ is the sequence of nonempty-open-subset-valued functions $\left\{ f_n\right\}_{n \in \mathbb N}$ such that $f_1$ gives the first choice $U_1$ of $\mathcal P_1$ and the remaining functions satisfy

\begin{aligned} U_n = f_n(U_1, V_1, \ldots, V_{n-1}) \subseteq V_{n-1}.\end{aligned}

Then

\left\{ f_n\right\}_{n \in \mathbb N}

is a winning strategy for

\mathcal P_1

if and only if

\bigcap_{n \in \mathbb N} U_n = \varnothing

We will prove the contrapositives in each direction. For the if side, assume that $X$ is not a Baire space. We will show that $\mathcal P_1$ has a winning strategy by constructing a sequence of nonempty open sets $\left\{ U_n\right\}_{n \in \mathbb N}$ such that their intersection is empty.

Since $X$ isn't a Baire space, Proposition 4.2 $(b)$ implies that there exists nonempty open set $U_1$ in $X$ and a sequence $\left\{ O_n\right\}_{n \in \mathbb N}$ of dense open sets in $X$ such that $U_1 \cap \left( \bigcap_{n \in \mathbb N} O_n \right) = \varnothing.$ This nonempty open set $U_1$ becomes the first move for $\mathcal P_1.$ Suppose $\mathcal P_2$ now plays $V_1 \subseteq U_1$ for any nonempty open set $V_1$ . Note that $V_1 \cap O_1 \neq \varnothing$ since $O_1$ is dense in $X.$ Let $\mathcal P_1$ play $U_2 = V_1 \cap O_1 \subseteq V_1.$ In the $n^{\text{th}}$ move, $\mathcal P_1$ plays $U_n = V_{n-1} \cap O_n \subseteq V_{n-1},$ which is nonempty because $O_n$ is dense in $X$ . But then we have

\begin{aligned} \bigcap_{n \in \mathbb N} U_n \subseteq U_1 \cap \left( \bigcap_{n \in \mathbb N} O_n \right) = \varnothing.\end{aligned}

For the other side, suppose $\mathcal P_1$ has a winning strategy $\left\{ f_n\right\}_{n \in \mathbb N}$ , and $U_1$ is his first move. We will show that $U_1$ is not Baire, which coupled with Proposition 4.4 will show that $X$ is not Baire. Then proceeding as we do in proofs of Theorems 6.4 and 6.7 we construct a clever family of open sets through which we construct a sequence of open dense sets $\left\{ G_n\right\}_{n \in \mathbb N}$ in $U_1.$ We then show that their intersection is empty, thereby showing that $U_1$ is not Baire.

APPLICATIONS

This section gives a few interesting applications of Baire category theorems. One of the most common applications of Baire category theorems is in proving the three big guns of functional analysis, namely Open Mapping Theorem, Closed Graph Theorem, Uniform Boundedness Principle. But these proofs can can be found very easily in any functional analysis text (see (Megginson, 1998) for example), so we will skip them.

Usually these applications follow a similar recipe: Suppose that $S$ is a desired property for the elements of some nonempty complete pseudo-metric space or some locally compact Hausdorff space $X$ . One way to show that $S$ is nonempty is to show that $X \setminus S$ is meager in $X$ . This is therefore usually an overkill, and why results like these are often surprising.

$\mathbb Q$ Is Not Homeomorphic To Any Complete Metric Space

It is well-known that $\mathbb Q$ , with the subspace topology with respect to $\mathbb R$ with its usual Euclidean topology, is not a complete metric space. But completeness is not a topological property as can be seen with the example of $\mathbb R$ and $(0,1)$ , both equipped with the usual topology, being homeomorphic under the homeomorphism

\begin{aligned} (0,1) \ni x \mapsto \tan\left( -\frac{\pi}{2} + \pi x \right) \in \mathbb R,\end{aligned}

but

\mathbb R

is complete while

(0,1)

is not. It is a simple consequence of Baire category theorem for complete metric spaces that

\mathbb Q

is not homeomorphic to any complete metric spaces.

Theorem 7.1:

\mathbb Q

is not homeomorphic to any complete metric spaces.

Let's first show that

\mathbb Q

is not a Baire space. Indeed, singletons in

\mathbb Q

are closed and have empty interior, and therefore

\mathbb Q

, which can be written as a countable union of all its singletons, cannot be Baire. Now by Proposition 4.5 and by Baire category theorem for complete metric spaces,

\mathbb Q

cannot be homeomorphic to any complete metric spaces.

Infinite-Dimensional Banach Spaces

We discuss another very simple application of Baire's category theorem to prove an important theorem.

Theorem 7.2: If

X

is an infinite dimensional Banach space, then every Hamel basis of

X

is uncountable.

Suppose to the contrary that $\left\{ v_n\right\}_{n \in \mathbb N}$ is a countable Hamel basis for an infinite dimensional Banach space $X$ . For each ${n \in \mathbb N}$ , define $F_n = \langle v_1, \ldots, v_n \rangle$ to be the span of the first $n$ vectors. Then by the definition of a Hamel basis, $X = \bigcup_{n \in \mathbb N} F_n$ . Recall at this point that $X$ is a complete metric space, and therefore a Baire space.

Now note that each $F_n$ , being a finite-dimensional normed space, is complete. A complete subspace of a complete metric space is closed, and therefore $F_n$ is closed in $X$ .

Next, we prove that each $F_n$ is nowhere dense. Since it is closed, we just need to show that $F_n$ has empty interior in $X$ . Suppose to the contrary that is not the case, and there exists an open ball $B_r(x_0) = \left\{ y \in X \,:\, \left\lVert y-x\right\rVert < r\right\}$ centered at some point $x_0 \in X$ for some $r > 0$ satisfying $B_r(x_0) \subseteq F_n$ . We now note that every point in $X$ can be rescaled and translated so that the transformation belongs to the ball $B_r(x_0)$ : if $x \in X$ , then $z = x_0 + \frac{r}{2\left\lVert x\right\rVert}x \in B_r(x_0)$ . Since $F_n$ is a subspace, this implies that $x = \frac{2\left\lVert x\right\rVert}{r}(z-x_0) \in F_n$ , implying $X \subseteq F_n$ , a contradiction.

These two facts together with the fact that $X$ is a Baire space imply that $X$ has empty interior, which is absurd.

A similar reasoning can be used to prove that the linear space of all polynomials in one variable $P$ is not a Banach space in any norm. This is because $P$ can be written as $P = \bigcup_{n \in \mathbb N} P_n$ , where $P_n$ is the subspace of $P$ containing polynomials of degree at most $n$ . Each $P_n$ is closed and nowhere dense in $P$ , and therefore $P$ cannot be a Baire space, which, in particular, means that it cannot be a Banach space.

A Generic Element Of $C[0,1]$ Is Nowhere Differentiable

Let us first make precise the meaning of "generic".

Definition 7.3: Let

X

be a topological space and

S \subseteq X

. If

X \setminus S

is meager, we say that

S\;

holds generically, or that a generic element of $X$ is in

S

. (Sometimes the word typical is used instead of generic.)

Definition 7.4: Let

C[0,1]

denote the collection of all real-valued continuous functions on

[0,1]

. We endow this collection with the sup norm,

\begin{aligned} \left\lVert f\right\rVert_\infty := \sup_{x \in [0,1]} \left\lvert f(x) \right\rvert, \quad f \in C[0,1].\end{aligned}

This makes

C[0,1]

into a Banach space (see (Megginson, 1998) for a proof).

We now prove that a generic element of $C[0,1]$ is nowhere differentiable. In fact, we will prove something stronger.

Theorem 7.5: Let

D_+

be the collection of all members

f

C[0,1]

for which there is a point

x_f \in [0,1)

at which

f

has a finite right-hand derivative. Then

D_+

is meager in

C[0,1]

We first note that $C[0,1]$ being a complete metric space is a Baire space by Theorem 5.6, and therefore the intersection of countably many dense open sets $\left\{ U_n\right\}_{n \in \mathbb N}$ in $C[0,1]$ is dense in $C[0,1]$ . This then implies that $C[0,1] \setminus \bigcap_{n \in \mathbb N} U_n$ is meager in $C[0,1]$ . Our strategy will be to define this sequence $\left\{ U_n\right\}_{n \in \mathbb N}$ in such a way that $D_+ \subseteq C[0,1] \setminus \bigcap_{n \in \mathbb N} U_n$ , thereby showing that $D_+$ is meager in $C[0,1]$ .

To this end, let

\begin{aligned} U_n = \left\{ f \in C[0,1] \,:\, \sup \left\{ \left\lvert \frac{f(y) - f(x)}{y-x} \right\rvert \,:\, y \in \left( x, x + \frac{1}{n} \right)\right\} > n, \; \forall \, x \in \left[0, 1 - \frac{1}{n} \right]\right\},\end{aligned}

and note that a function

f \in C[0,1]

with a finite right-hand derivative at some point in

[0,1)

cannot lie in every

U_n

. Therefore,

D_+ \subseteq C[0,1] \setminus \bigcap_{n \in \mathbb N} U_n

. What remains to show that each

U_n

is open and dense in

C[0,1]

. Fix an arbitrary

n_0 \in \mathbb N

$U_{n_0}$ is open in $C[0,1]$ : We show this by showing that $C[0,1] \setminus U_{n_0}$ is closed in $C[0,1]$ . Suppose $\left\{ f_m\right\}_{m \in \mathbb N}$ is a sequence in $C[0,1] \setminus U_{n_0}$ that converges to $f_0 \in C[0,1]$ . Since $C[0,1]$ is a metric space, to show $C[0,1] \setminus U_{n_0}$ is closed in $C[0,1]$ , it is sufficient to show that $f_0 \in C[0,1] \setminus U_{n_0}$ . By the definition of $U_{n_0}$ , for each $m \in \mathbb N$ , there exists $x_m \in [0, 1 - 1/n_0]$ such that

\begin{aligned} \left\lvert \frac{f_m(y) - f_m(x_m)}{y-x_m} \right\rvert \le n_0, \quad \forall \, y \in \left( x_m, x_m + \frac{1}{n_0} \right).\end{aligned}

The sequence

\left\{ x_m\right\}_{m \in \mathbb N}

lies in the compact set

[0, 1-1/n_0]

, and therefore there exists a convergent subsequence, say

\left\{ x_{m_k}\right\}_{k \in \mathbb N}

converging to

x_0 \in [0, 1-1/n_0]

. If

y \in \left( x_0, x_0 + 1/n_0 \right)

, then for

k

large enough

y \in \left( x_{m_k}, x_{m_k} + 1/n_0 \right)

. Since the functions

\left\{ f_m\right\}_{m \in \mathbb N}

are continuous, we have

\begin{aligned} \left\lvert \frac{f_{m_k}(y) - f_{m_k}(x_{m_k})}{y-x_{m_k}} \right\rvert \xrightarrow{k \to \infty} \left\lvert \frac{f_0(y) - f_0(x_0)}{y-x_0} \right\rvert.\end{aligned}

Therefore,

\left\lvert \frac{f_0(y) - f_0(x_0)}{y-x_0} \right\rvert \ge n_0

, and we have

f_0 \in C[0,1] \setminus U_{n_0}

$U_{n_0}$ is dense in $C[0,1]$ : Recall the Stone-Weierstrass theorem (Folland, 1999) which implies that polynomials on $[0,1]$ (with the subspace topology), denoted $P[0,1]$ , are dense in $C[0,1]$ . Therefore, in light of Proposition 2.6, it is sufficient to show that $U_{n_0}$ is dense in $P[0,1]$ .

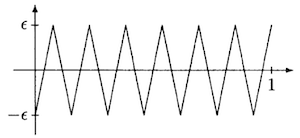
Given $\epsilon > 0$ and $M > 0$ , Figure 1 shows how to construct a function in $C[0,1]$ that has norm $\epsilon$ and absolute value of right-hand derivative greater than $M$ at each point of $[0,1)$ .

Since each polynomial $p \in P[0,1]$ has a bounded right-hand derivative on $[0,1)$ , it follows that a function of the form in Figure 1 can be added to $p$ to obtain a member $u \in U_{n_0}$ such that $\left\lVert u-p\right\rVert_\infty \le \epsilon$ . This shows that $U_{n_0}$ is dense in $P[0,1]$ .

A Special Infinitely Differentiable Function

We end our applications with a very curious result.

Theorem 7.6: If

f \colon \mathbb R \to \mathbb R

is infinitely differentiable, and for every

x \in \mathbb R

there is a nonnegative integer

n

such that

f^{(n)}(x) = 0

, then

f

is a polynomial.

We will prove by contradiction. So suppose $f$ is not a polynomial. Define the set

\begin{aligned} X = \left\{ x \in \mathbb R \,:\, \text{for every interval } (a,b) \text{ containing } x \text{, the restriction } f \restriction_{(a,b)} \text{ is not a polynomial}\right\},\end{aligned}

and note that since

f

is not a polynomial,

X

is nonempty. It is easy to see that

X

is closed with all of its points being limit points. Define the sequence of sets

\left\{ S_n\right\}_{n \in \mathbb N}

\begin{aligned} S_n = \left\{ x \,:\, f^{(n)}(x) = 0\right\},\end{aligned}

and note that for each

{n \in \mathbb N}

, by the continuity of

f^{(n)}

S_n

is closed. Using the property of

f

in the hypothesis, we can write

\begin{aligned} X = \bigcup_{n \in \mathbb N} \left( X \cap S_n \right).\end{aligned}

Now note that

X

being closed is also complete, and therefore by the Baire category theorem is a Baire space. Since each

X \cap S_n

is closed in

X

, this implies that there exists

N \in \mathbb N

such that

X \cap S_N

is not nowhere dense in

X

. Equivalently, this means there exists a nonempty open subset of

X

contained in

X \cap S_N

. So there exists an interval

(a,b)

such that

(i) $X \cap (a,b)$ is nonempty (note that it's open in $X$ ), and

(ii) $X \cap (a,b) \subseteq S_N$ .

Suppose $x \in X \cap (a,b)$ . Then since $x$ is a limit point of $X \cap (a,b)$ , there exists a sequence $\left\{ x_n\right\}_{n \in \mathbb N} \subseteq X \cap (a,b)$ converging to $x$ . Property $(ii)$ implies that $f^{(N)}(x_n) = 0$ for all ${n \in \mathbb N}$ . Using the definition of derivative, this implies $f^{(N+1)}(x) = 0$ showing $x \in S_{N+1}$ . Proceeding similarly we get,

(iii) $x \in S_m$ for all $m \ge N$ and every $x \in X \cap (a,b)$ .

Consider any maximal interval $(c,d) \subseteq \left( (a,b) \setminus X \right)$ . Since $(c,d)$ lies outside $X$ , $f$ is a polynomial on $(c,d)$ , say of degree $k$ . This implies that $f^{(k)} \neq 0$ on $(c,d)$ . Continuity of $f^{(k)}$ implies that in fact $f^{(k)} \neq 0$ on $[c,d]$ . Since one of $c$ or $d$ must be in $X$ , using property $(iii)$ this implies $k < N$ .

This along with property $(iii)$ shows that $f^{(N)} = 0$ on the full interval $(a,b)$ . But then this means the restriction $f \restriction_{(a,b)}$ is a polynomial which contradicts property $(i)$ .

REFERENCES

Körner, T. (2008). Linear Analysis. Course notes for the Part II course Linear Analysis at Cambridge University.
Rota, G. (2008). Indiscrete Thoughts. Modern Birkhäuser Classics. Birkhäuser Boston.
Tao, T. (2021). Exploring the toolkit of Jean Bourgain. Bulletin of the American Mathematical Society, 58(2):155–171.
Munkres, J. R. (2000). Topology. Prentice Hall, Incorporated, 2nd edition.
Willard, S. (2004). General Topology. Addison-Wesley series in mathematics. Dover Publications.
Engelking, R. (1989). General Topology. Sigma series in pure mathematics. Heldermann.
Berberian, S. K. (1974). Lectures in functional analysis and operator theory. Springer-Verlag.
Oxtoby, J. (1971). Measure and Category: A Survey of the Analogies between Topological and Measure Spaces. Graduate Texts in Mathematics. Springer New York.
Haworth, R. C. and McCoy, R. A. (1977). Baire spaces. Instytut Matematyczny Polskiej Akademi Nauk.
Cohen, P. E. (1976). Products of baire spaces. Proceedings of the American Mathematical Society, Volume 55, Number 1.
Telegarsky R. (1987). Topological games: On the 50th anniversary of the Banach Mazur game. Rocky Mountain J. Math. 17(2): 227-276 (Spring 1987).
Oxtoby, J. C. (1957). The Banach-Mazur game and Banach Category Theorem, pages 159– 164. Contributions to the Theory of Games (Annals of Math. Studies-39), Volume III. Princeton University Press.
Choquet, G. (1969). Lectures on Analysis, Vol. I. Lectures on Analysis. W.A. Benjamin, New York and Amsterdam.
Megginson, R. (1998). An Introduction to Banach Space Theory. Graduate Texts in Mathematics. Springer New York.
Folland, G. B. (1999). Real Analysis: Modern Techniques and Their Applications. Pure and Applied Mathematics, Wiley, 2nd edition.